Imagine you need a relatively compact data structure for quickly checking membership of mostly-consecutive non-negative integers. (If this sounds really specific, it is because it is precisely what I needed for a particular project.)
The Ruby standard library contains a Set class which may be a good starting point. Set is actually implemented as a Hash with the Set elements as keys and true as the values. Thus the overhead for storing a value in the Set is essentially only the value itself since all keys point to the same true object. Assuming a 64-bit machine, the overhead will be 64 bits per value. This seems reasonable, but given the specific limitations of the values we wish to store, perhaps we can do better?
Bit Sets
A bit set is a compact data structure of binary values where membership is indicated by setting a bit to 1. The position of the bit indicates the element value. For example, the second bit from the right might be used to indicate whether or not the value 1 is in the set.
One method to determine membership is to AND the bit set with a mask with only the desired bit set to 1. If the result is 0, the value is not in the set. If it is any other result (actually the mask itself, but the zero check is sufficinet), the value is a member of the set.
In Ruby, this looks like
1
| |
For example, to check if the value 4 is in the set, we use the mask 00010000 (the 5th bit from the right is set to 1) which is the decimal value 8:
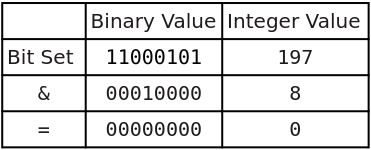
Since the result is zero, we know the value 4 is not in the set.
If we check for the value 6, the result is not zero, indicating the value is a member of the set:
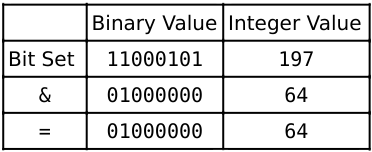
Now, instead of 64 bits per value, it only requires a single bit! Now we just need to put a lot of bits together, either by using a long string or a bunch of integers in an array.
Sparse Bit Sets
The problem with a long binary string or an array of integers is that membership is entirely position-based. To store the value 1000, the data structure requires 1001 bits, all but one of which is set to 0. This is quite inefficient, especially for very large values.
One solution is to create a sparse bit set by combining a hash table with bit sets as values. The hash table keys provide fast look up of the correct bit set, then the bit set is checked for the desired element. The keys indicate the lowest value stored in the bit set (e.g., the decimal key 4 pointing to the binary bit set 00000001 would mean the value 4 is in the set).
Below is an example of a hash table using integer keys and 8 bit integers for the bit sets:
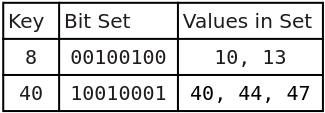
The average overhead is ⌊(m * n) / w⌋ + m bits, where m is the number of values (assumed to be consecutive), w is the number of bits per bit set, and n is the number of bits per key. In 64-bit Ruby, if we use integers for the bit sets, n = 64 and w = 62*. This works out to an average of 2 bits per value in the set. Of course, a single value incurs the overhead of both the key and the bit set: 128 bits! But if there are many consecutive values, the cost per value begins to shrink. For example, the numbers 0 to 61 can be stored in a single bit set, so 62 values can be stored in the 128 bits and we are back to about 2 bits per value.
Note that while it is best to use consecutive values which fit neatly into the bit sets (in this case, runs of 62 integers), the sequences can start and end at arbitrary points with only a little “wasted” overhead. To store just the number 1000, we now only need 128 bits, not 1001.
On top of the space savings, the membership checks remain fast. Still assuming 64-bit Ruby, to determine if a value is in the table look up index i = value / 61. Then check the bit set with bitset & (1 << (value % 61) != 0 as previously. (The divisor is 61 because there are 62 bits, but the values are 0 to 61).
Space Efficiency
I have implemented a Ruby version of the data structure described above which I call the Dumb Numb Set (DNS).
To measure the space used by the bit sets, we compare the Marshal data size for the bit sets versus regular Hashes (using true for all values, just like a Ruby Set).
These are the results for perfectly ordered data on a 64-bit version of Ruby 1.9.3 (size is number of bytes):
1 2 3 4 5 6 7 8 9 10 11 12 | |
At 1 billion items, my machine ran out of memory.
For a single item, as expected, overhead in the DNS is quite high. But for as little as 100 items in the set, the DNS is considerably more compact.
This is, however, the best case scenario for the DNS. Less perfectly dense values cause it to be less efficient. For very sparse values, a Hash/Set is probably a better choice.
Even Better Space Efficiency
It may not surprise you to find out I was very interested in minimizing the serialized version of the sparse bit set for sending it over a network. In investigating easy but compact ways of doing so, I realized the Marshal data for Hashes and integers is not very compact, especially for large integers.
Fortunately, there is an existing solution for this scenario called MessagePack. For storing 1 million values, serialized size is reduced from 245,565 to 196,378 bytes (20%). The DNS will use MessagePack automatically if it is installed.
Performance
Somewhat surprisingly, the DNS is quite fast even when compared to MRI Ruby’s Hash implementation.
With MRI Ruby 1.9.3p448 (x86_64) and 1 million values:
1 2 3 4 5 6 7 8 9 10 11 | |
The only operation slower than a regular Hash is inserting many random values. All other operations are roughly equal.
Conclusion
For my specific scenario, a simple custom data structure was just as fast as a built-in data structure, but required significantly less space for the expected use case.
There are other solutions for this type of problem, but it should be noted I only really care about fast insertion, fast membership checks, and compact representation. Additionally, values may be very large, although I attempt to keep them within the Fixnum range for Ruby (i.e. less than 262 - 1). This rules out some implementations which require arrays the size of the maximum value!
I also did not want to deal with compression schemes, of which there are quite a few, since my sets were going to be dynamic. I imagine there are very efficient implementations for fixed data sets.
Footnote: Integer Size in Ruby
Integers in 32-bit MRI Ruby only have 30 bits available, and in 64-bit MRI Ruby they only have 62 bits available:
1 2 3 4 5 | |